Meta-analysis: introduction
A meta-analysis integrates the quantitative findings from separate but similar studies and provides a numerical estimate of the overall effect of interest (Petrie et al., 2003).
Different weights are assigned to the different studies for calculating the summary or pooled effect. The weighing is related with the inverse of the standard error (and therefore indirectly to the sample size) reported in the studies. Studies with smaller standard error and larger sample size are given more weight in the calculation of the pooled effect size.
The effect of interest can be:
- an average of a continuous variable
- a correlation between two variables
- an odds ratio, suitable for analyzing retrospective studies
- a relative risk (risk ratio) or risk difference, suitable for analyzing prospective studies
- a proportion
- the area under the ROC curve
The agreement or disagreement between the studies is examined using different measures of heterogeneity.
Fixed and random effects model
Under the fixed effects model, it is assumed that the studies share a common true effect, and the summary effect is an estimate of the common effect size.
Under the random effects model the true effects in the studies are assumed to vary between studies and the summary effect is the weighted average of the effects reported in the different studies (Borenstein et al., 2009).
The random effects model will tend to give a more conservative estimate (i.e. with wider confidence interval), but the results from the two models usually agree when there is no heterogeneity. When heterogeneity is present (see below) the random effects model should be the preferred model.
Heterogeneity
Example:

Cochran's Q
Q is the weighted sum of squares on a standardized scale. It is reported with a P value with low P-values indicating presence of heterogeneity. This test however is known to have low power to detect heterogeneity and it is suggested to use a value of 0.10 as a cut-off for significance (Higgins et al., 2003). Conversely, Q has too much power as a test of heterogeneity if the number of studies is large.
I2 statistic
I2 is the percentage of observed total variation across studies that is due to real heterogeneity rather than chance. It is calculated as I2 = 100% x (Q - df)/Q, where Q is Cochran's heterogeneity statistic and df the degrees of freedom. Negative values of I2 are put equal to zero so that I2 lies between 0% and 100%. A value of 0% indicates no observed heterogeneity, and larger values show increasing heterogeneity (Higgins et al., 2003).
According to Higgins & Green (2011) I2 can be interpreted as follows:
| 0% to 40% | might not be important |
| 30% to 60% | may represent moderate heterogeneity |
| 50% to 90% | may represent substantial heterogeneity |
| 75% to 100% | considerable heterogeneity |
Publication bias
All MedCalc's meta-analysis reports include two tests to detect possible publication bias: Egger's test (Egger et al., 1997) and Begg's rank test (Begg and Mazumdar, 1994).
Egger's test is a test for the Y intercept = 0 from a linear regression of normalized effect estimate (estimate divided by its standard error) against precision (reciprocal of the standard error of the estimate).
Begg's test assesses if there is a significant correlation between the ranks of the standardized effect sizes and the ranks of their variances.
For both tests, when the (two-sided) P-value is low, this is an indication of publication bias.
Note that the power of both methods to detect bias will be low with small numbers of studies.
Example:
Forest plot
The results of the different studies, with 95% CI, and the overall effect (under the fixed and random effects model) with 95% CI are illustrated in a graph called "forest plot", for example:
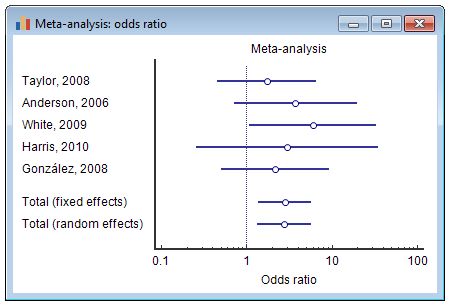
In this example the markers representing the effect size all have the same size. Optionally, the marker size may vary in size according to the weights assigned to the different studies. In addition, the pooled effects can be represented using a diamond. The location of the diamond represents the estimated effect size and the width of the diamond reflects the precision of the estimate, for example:

Funnel plot
A funnel plot (Egger et al., 1997) is a graphical tool for detecting bias in meta-analysis.
In a funnel plot treatment effect is plotted on the horizontal axis and MedCalc plots the standard error on the vertical axis (Sterne & Egger, 2001).
The vertical line represents the summary estimated derived using fixed-effect meta-analysis.
Two diagonal lines represent (pseudo) 95% confidence limits (effect ± 1.96 SE) around the summary effect for each standard error on the vertical axis. These show the expected distribution of studies in the absence of heterogeneity or of selection bias. In the absence of heterogeneity, 95% of the studies should lie within the funnel defined by these diagonal lines.
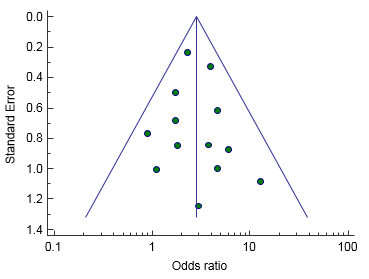 |
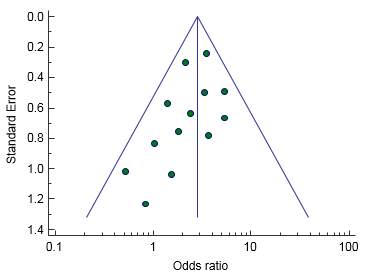 |
| Example of symmetrical funnel plot | Example of asymmetrical funnel plot |
Publication bias results in asymmetry of the funnel plot. If publication bias is present, the smaller studies will show the larger effects. See Sterne et al. (2011) for interpreting funnel plot asymmetry. The funnel plot may not always be a reliable tool, in particular when the number of studies included in the analysis is small.
Meta-analysis in MedCalc
- Continuous measure
- Correlation
- Proportion
- Relative risk
- Risk difference
- Odds ratio
- Area under ROC curve
- Generic inverse variance method (if none of the above is applicable)
Literature
- Begg CB, Mazumdar M (1994) Operating characteristics of a rank correlation test for publication bias. Biometrics 50:1088–1101.
- Borenstein M, Hedges LV, Higgins JPT, Rothstein HR (2009) Introduction to meta-analysis. Chichester, UK: Wiley.
- Egger M, Smith GD, Schneider M, Minder C (1997) Bias in meta-analysis detected by a simple, graphical test. BMJ 315: 629–634.
- Higgins JPT, Green S (eds) (2011) Cochrane Handbook for Systematic Reviews of Interventions. Version 5.1.0. Identifying and measuring heterogeneity
- Higgins JP, Thompson SG, Deeks JJ, Altman DG (2003) Measuring inconsistency in meta-analyses. BMJ 327:557-560.
- Petrie A, Bulman JS, Osborn JF (2003) Further statistics in dentistry. Part 8: systematic reviews and meta-analyses. British Dental Journal 194:73-78.
- Sterne JA, Egger E (2001) Funnel plots for detecting bias in meta-analysis: guidelines on choice of axis. Journal of Clinical Epidemiology 54:1046–1055.
- Sterne JA, Sutton AJ, Ioannidis JP et al. (2011) Recommendations for examining and interpreting funnel plot asymmetry in meta-analyses of randomised controlled trials. BMJ 2011;343:d4002.
