ROC curve analysis in MedCalc

Command:

Statistics ROC curves ROC curve analysis

Description

Allows to create ROC curve and a complete sensitivity/specificity report. The ROC curve is a fundamental tool for diagnostic test evaluation.

In a ROC curve the true positive rate (Sensitivity) is plotted in function of the false positive rate (100-Specificity) for different cut-off points of a parameter. Each point on the ROC curve represents a sensitivity/specificity pair corresponding to a particular decision threshold. The area under the ROC curve is a measure of how well a parameter can distinguish between two diagnostic groups (diseased/normal).

Theory summary

The diagnostic performance of a test, or the accuray of a test to discriminate diseased cases from normal cases is evaluated using Receiver Operating Characteristic (ROC) curve analysis (Metz, 1978; Zweig & Campbell, 1993). ROC curves can also be used to compare the diagnostic performance of two or more laboratory or diagnostic tests (Griner et al., 1981).

When you consider the results of a particular test in two populations, one population with a disease, the other population without the disease, you will rarely observe a perfect separation between the two groups. Indeed, the distribution of the test results will overlap, as shown in the following figure.

For every possible cut-off point or criterion value you select to discriminate between the two populations, there will be some cases with the disease correctly classified as positive (TP = True Positive fraction), but some cases with the disease will be classified negative (FN = False Negative fraction). On the other hand, some cases without the disease will be correctly classified as negative (TN = True Negative fraction), but some cases without the disease will be classified as positive (FP = False Positive fraction).

Schematic outcomes of a test

The different fractions (TP, FP, TN, FN) are represented in the following table.

	Disease
Test	Present	n		Absent	n		Total
Positive	True Positive (TP)	a		False Positive (FP)	c		a + c
Negative	False Negative (FN)	b		True Negative (TN)	d		b + d
Total		a + b			c + d

The following statistics can be defined:

Sensitivity	a a + b		Specificity	d c + d
Positive Likelihood Ratio	Sensitivity 1 - Specificity		Negative Likelihood Ratio	1 - Sensitivity Specificity
Positive Predictive Value	a a + c		Negative Predictive Value	d b + d

• Sensitivity: probability that a test result will be positive when the disease is present (true positive rate, expressed as a percentage).
  = a / (a+b)
• Specificity: probability that a test result will be negative when the disease is not present (true negative rate, expressed as a percentage).
  = d / (c+d)
• Positive likelihood ratio: ratio between the probability of a positive test result given the presence of the disease and the probability of a positive test result given the absence of the disease, i.e.
  = True positive rate / False positive rate = Sensitivity / (1-Specificity)
• Negative likelihood ratio: ratio between the probability of a negative test result given the presence of the disease and the probability of a negative test result given the absence of the disease, i.e.
  = False negative rate / True negative rate = (1-Sensitivity) / Specificity
• Positive predictive value: probability that the disease is present when the test is positive (expressed as a percentage).
  = a / (a+c)
• Negative predictive value: probability that the disease is not present when the test is negative (expressed as a percentage).
  = d  / (b+d)

Sensitivity and specificity versus criterion value

When you select a higher criterion value, the false positive fraction will decrease with increased specificity but on the other hand the true positive fraction and sensitivity will decrease:

When you select a lower criterion value, then the true positive fraction and sensitivity will increase. On the other hand the false positive fraction will also increase, and therefore the true negative fraction and specificity will decrease.

The ROC curve

In a Receiver Operating Characteristic (ROC) curve the true positive rate (Sensitivity) is plotted in function of the false positive rate (100-Specificity) for different cut-off points. Each point on the ROC curve represents a sensitivity/specificity pair corresponding to a particular decision threshold. A test with perfect discrimination (no overlap in the two distributions) has a ROC curve that passes through the upper left corner (100% sensitivity, 100% specificity). Therefore the closer the ROC curve is to the upper left corner, the higher the overall accuracy of the test (Zweig & Campbell, 1993).

How to enter data for ROC curve analysis

In order to perform ROC curve analysis in MedCalc you should have a measurement of interest (= the parameter you want to study) and an independent diagnosis which classifies your study subjects into two distinct groups: a diseased and non-diseased group. The latter diagnosis should be independent from the measurement of interest.

In the spreadsheet, create a column DIAGNOSIS and a column for the variable of interest, e.g. TEST1. For every study subject enter a code for the diagnosis as follows: 1 for the diseased cases, and 0 for the non-diseased or normal cases. In the TEST1 column, enter the measurement of interest (this can be measurements, grades, etc. - if the data are categorical, code them with numerical values).

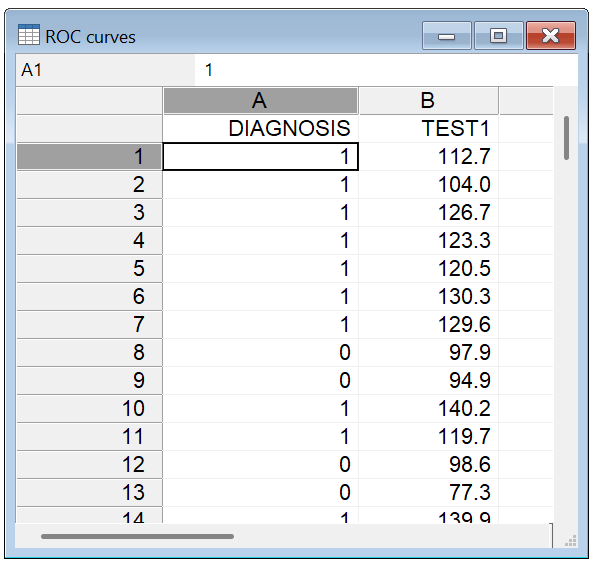
Required input

Complete the ROC curve analysis dialog box as follows:

Data

• Variable: identify the variables under study.
• Classification variable: select or enter a a dichotomous variable indicating diagnosis (0=negative, 1=positive). If diagnosis is coded differently than using the values 0 and 1, you can use the IF function to transform the codes into 0 and 1 values, e.g. IF(RESULT="pos",1,0).
• Select: (optionally) a selection criterion in order to include only a selected subgroup of cases (e.g. AGE>21, SEX="Male").

Methodology:

• DeLong et al.: use the method of DeLong et al. (1988) for the calculation of the Standard Error of the Area Under the Curve (recommended).
• Hanley & McNeil: use the method of Hanley & McNeil (1982) for the calculation of the Standard Error of the Area Under the Curve.
• Binomial exact Confidence Interval for the AUC: calculate an exact Binomial Confidence Interval for the Area Under the Curve (recommended). If this option is not selected, the Confidence Interval is calculated as AUC ± 1.96 its Standard Error.

Options

• Disease prevalence: if the sample sizes in the positive and the negative group do reflect the real prevalence of the disease, this can be indicated in the dialog box. Alternatively you can enter the disease prevalence, expressed as a percentage. Clinically, the disease prevalence is the same as the probability of disease being present before the test is performed. If the disease prevalence is unknown, or irrelevant for the current statistical analysis, you can ignore these fields. In this case the program will not calculate predictive values.
• List criterion values with test characteristics: option to create a list of criterion values corresponding with the coordinates of the ROC curve, with associated sensitivity, specificity, likelihood ratios and predictive values (if disease prevalence is known).
  • Include all observed criterion values: When you select this option, the program will list sensitivity and specificity for all possible threshold values. If this option is not selected, then the program will only list the more important points of the ROC curve: for equal sensitivity/specificity it will give the threshold values (criterion values) with the highest specificity/sensitivity.
• 95% Confidence Interval for sensitivity/specificity, likelihood ratio and predictive values: select the Confidence Intervals you require.

Graphs

• Select Display ROC curve window to obtain the ROC curve in a separate window.
  Options:
  • mark points corresponding to criterion values.
  • display 95% Confidence Bounds for the ROC curve (Hilgers, 1991).

A few moments after you have pressed the Enter key, or clicked the OK button, the following appears in the results window. The report may consist of several pages of text, and press the Page down key to see the next pages of the report.

Results

First the program displays the number of observations in the two groups. Concerning sample size, it has been suggested that meaningful qualitative conclusions can be drawn from ROC experiments performed with a total of about 100 observations (Metz, 1978). A minimum of 50 cases may be required in each of the two groups, so that 1 case represents not more than 2% of the observations.

The value for the area under the ROC curve can be interpreted as follows: an area of 0.84, for example, means that a randomly selected individual from the positive group has a test value larger than that for a randomly chosen individual from the negative group in 84% of the time (Zweig & Campbell, 1993). When the variable under study can not distinguish between the two groups, i.e. where there is no difference between the two distributions, the area will be equal to 0.5 (the ROC curve will coincide with the diagonal). When there is a perfect separation of the values of the two groups, i.e. there no overlapping of the distributions, the area under the ROC curve equals 1 (the ROC curve will reach the upper left corner of the graph).

The 95% Confidence Interval is the interval in which the true (population) Area under the ROC curve lies with 95% confidence..

The P-value is the probability that the sample Area under the ROC curve (0.947 in the example) is found when in fact, the true (population) Area under the ROC curve is 0.5 (null hypothesis: Area = 0.5). If P is low (P<0.05) then it can be concluded that the Area under the ROC curve is significantly different from 0.5 and that therefore there is evidence that the laboratory test does have an ability to distinguish between the two groups.

The next section of the results window lists the different selection criteria or cut-off values with their corresponding sensitivity and specificity of the test, and the positive (+LR) and negative likelihood ratio (LR).

If the disease prevalence is known, the program also reports the positive predictive value (+PV) and negative predictive value (-PV):

When you did not select the option Include all observed criterion values, the program only lists the more important points of the ROC curve: for equal sensitivity (resp. specificity) it gives the threshold value (criterion value) with the highest specificity (resp. sensitivity). When you do select the option Include all observed criterion values, the program will list sensitivity and specificity for all possible threshold values.

The criterion value indicated with a * sign is the value corresponding with the maximum of the Youden index:

J = max[SE_i + SP_i - 1]

where SE_i and SP_i are the sensitivity and specificity over all possible threshold values. This value corresponds with the point on the ROC curve farthest from the diagonal line.

• When you select a lower criterion value, then the true positive fraction and sensitivity will increase. On the other hand the false positive fraction will also increase, and therefore the true negative fraction and specificity will decrease.
• When you select a higher criterion value, the false positive fraction will decrease with increased specificity but on the other hand the true positive fraction and sensitivity will decrease.
• If a test is used for the purpose of screening, then a cut-off value with a higher sensitivity and negative predictive value must be selected. In order to confirm the disease, the cases positive in the screening test can be tested again with a different test. In this second test, a high specificity and positive predictive value are required (Griner et al., 1981).

Importance of disease prevalence

Whereas sensitivity and specificity, and therefore the ROC curve, and positive and negative likelihood ratio are independent of the prevalence of the disease, positive and negative predictive values are highly dependent on the proportions of subjects who do and do not have the disease (prior probability of disease), and hence on the population studied.

Clinically, the disease prevalence is the same as the probability of disease being present before the test is performed.

If the sample sizes in the positive and the negative group do not correspond to the real prevalence of the disease, indicate this in the dialog box by deselecting the corresponding option:

In this case the program will not calculate the positive and negative predictive values.

However, if you do know the disease prevalence in the population, you can enter the percentage in the dialog box:

Display ROC curve

The ROC curve will be displayed in a second window when you have selected the corresponding option in the dialog box.

In a ROC curve the true positive rate (Sensitivity) is plotted in function of the false positive rate (100-Specificity) for different cut-off points. Each point on the ROC curve represents a sensitivity/specificity pair corresponding to a particular decision threshold. A test with perfect discrimination (no overlap in the two distributions) has a ROC curve that passes through the upper left corner (100% sensitivity, 100% specificity). Therefore the closer the ROC curve is to the upper left corner, the higher the overall accuracy of the test (Zweig & Campbell, 1993).

When you click on a specific point of the ROC curve, the corresponding cut-off point with sensitivity and specificity will be displayed.

Presentation of results

The prevalence of a disease may be different in different clinical settings. For instance the pre-test probability for a positive test will be higher when a patient consults a specialist than when he consults a general practitioner. Since positive and negative predictive values are sensitive to the prevalence of the disease, it would be misleading to compare these values from different studies where the prevalence of the disease differs, or apply them in different settings.

The data from the results window can be summarized in a table. The sample size in the two groups should be clearly stated. The table can contain a column for the different criterion values, the corresponding sensitivity (with 95% CI), specificity (with 95% CI), and possibly the positive and negative predictive value. The table should not only contain the test's characteristics for one single cut-off value, but preferably there should be a row for the values corresponding with a sensitivity of 90%, 95% and 99%, specificity of 90%, 95% and 99%, and the value corresponding with the highest accuracy (maximum sensitivity and specificity as indicated with a * mark in the results window).

With these data, any reader can calculate the negative and positive predictive value applicable in his own clinical setting when the knows the prior probability of disease (pre-test probability or prevalence of disease) in this setting, by the following formula's based on Bayes' theorem:

and

The negative and positive likelihood ratio must be handled with care because they are easily and commonly misinterpreted.

Literature

• DeLong ER, DeLong DM, Clarke-Pearson DL (1988) Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 44:837-845. [Abstract]
• Griner PF, Mayewski RJ, Mushlin AI, Greenland P (1981) Selection and interpretation of diagnostic tests and procedures. Annals of Internal Medicine 94:555-600. [Abstract]
• Hanley JA, Hajian-Tilaki KO (1997) Sampling variability of nonparametric estimates of the areas under receiver operating characteristic curves: an update. Academic Rediology 4:49-58. [Abstract]
• Hanley JA, McNeil BJ (1982) The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143:29-36. [Abstract]
• Hilgers RA (1991) Distribution-free confidence bounds for ROC curves. Methods of Information in Medicine 30:96-101. [Abstract]
• Metz CE (1978) Basic principles of ROC analysis. Seminars in Nuclear Medicine 8:283-298. [Abstract]
• Zweig MH, Campbell G (1993) Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine. Clinical Chemistry 39:561-577. [Abstract]

See also

• Interactive dot diagram
• Plot versus criterion values
• Predictive values
• Interval likelihood ratios
• Comparison of ROC curves
• Format graph
• Graph legend
• Add graphical objects
• Reference lines

External links

• Receiver operating characteristic on Wikipedia.