Relative risk - Number Needed to Treat
| Command: | Tests |
Description
Allows to calculate a relative risk (or risk ratio). The relative risk is the ratio of the proportions of cases having a positive outcome in two groups included in a prospective study.
In a prospective study cases are allocated to two groups and it is observed how many times the event of interest occurs.
The program optionally also calculates the Number Needed to Treat (NNT) with its 95% confidence interval.
This test is not performed on data in the spreadsheet, but on numbers you enter in a dialog box.
Required input
In the dialog box enter the number of cases with a positive (bad) and negative (good) outcome in the exposed and control groups.
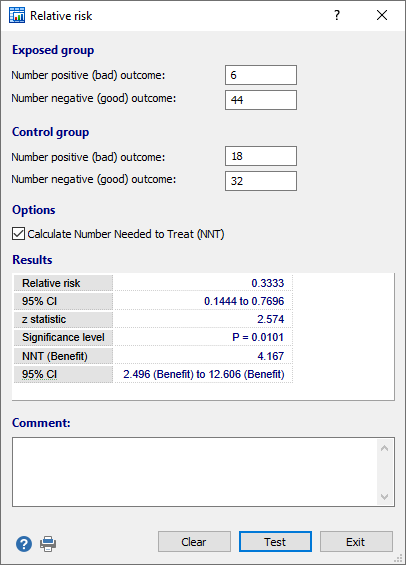
Click Test to perform the test.
Relative risk
The program calculates the relative risk and a 95% confidence interval (Altman 1991, Daly 1998, Sheskin 2011). The relative risk is the ratio of the proportions of cases having a positive outcome in the two groups. If the value 1 is not in the range of the confidence interval, it can be concluded that the proportions are significantly different in the two groups, and there is an increased risk in one group compared to the other.
In the example, there was a positive outcome in 6 cases and a negative outcome in 44 cases in a group given treatment A. In a second group without treatment, 18 cases had a positive and 32 cases had a negative outcome.
The risk in the first group was 0.12 (6/50) and in the second group 0.36 (18/50). The relative risk for a positive outcome was 0.3333 (0.12/0.36) with a 95% confidence interval ranging from 0.1444 to 0.7696; the z-statistic is 2.574 and the associated P-value is 0.01. The conclusion is that there is a 3-fold decreased risk in the treatment A group, and this decrease is statistically significant (P=0.01).
Number Needed to Treat (NNT)
The number needed to treat (NNT) is the estimated number of patients who need to be treated with the new treatment rather than the standard treatment (or no treatment) for one additional patient to benefit (Altman 1998).
A negative number for the number needed to treat has been called the number needed to harm.
MedCalc uses the terminology suggested by Altman (1998) with NNT(Benefit) and NNT(Harm) being the number of patients needed to be treated for one additional patient to benefit or to be harmed respectively.
The 95% confidence interval is calculated according to Daly (1998) and is reported as suggested by Altman (1998).
In an optional Comment input field you can enter a comment or conclusion that will be included on the printed report.
Literature
- Altman DG (1991) Practical statistics for medical research. London: Chapman and Hall.
- Altman DG (1998) Confidence intervals for the number needed to treat. British Medical Journal 317: 1309-1312.
- Daly LE (1998) Confidence limits made easy: interval estimation using a substitution method. American Journal of Epidemiology 147: 783-790.
- Sheskin DJ (2011) Handbook of parametric and non-parametric statistical procedures. 5th ed. Boca Raton: Chapman & Hall /CRC.
