Paired samples t-test

Command

Statistics T-tests Paired samples t-test

Description

The paired samples t-test is used to test the null hypothesis that the average of the differences between a series of paired observations is zero. Observations are paired when, for example, they are performed on the same samples or subjects.

Required input

Select the variables for sample 1 and sample 2, and a possible selection criterion for the data pairs. You can use the button to select variables and selection criteria in the variables list.

Options

Logarithmic transformation: if the data require a logarithmic transformation (e.g. when the data are positively skewed), select the Logarithmic transformation option.

Results

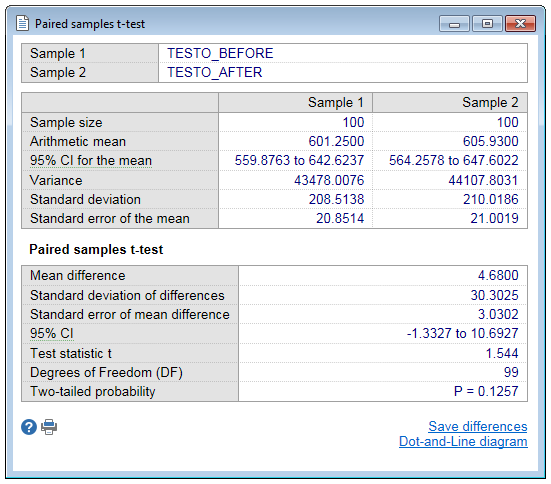
The program displays the summary statistics of the two samples followed by the mean of the differences between the paired observations, and the standard deviation of these differences, followed by a 95% confidence interval for the mean.

Note that the sample size will always be equal (only cases are included with data available for the two variables).

Next the result of the null hypothesis test is displayed. If the calculated P-value is less than 0.05, the conclusion is that the mean difference between the paired observations is statistically significantly different from 0.

Log transformation

If you selected the Log transformation option, the program performs the calculations on the logarithms of the observations, but reports the back-transformed summary statistics.

For the paired samples t-test, the mean difference and 95% confidence are given on the log-transformed scale.

Next, the results of the t-test are transformed back and the interpretation is as follows: the back-transformed mean difference of the logs is the geometric mean of the ratio of paired values on the original scale (Altman, 1991).

Literature

• Altman DG (1991) Practical statistics for medical research. London: Chapman and Hall.

See also

• Independent samples t-test

External links

• Student's t-test on Wikipedia.