Cochran–Mantel–Haenszel test
| Command: | Statistics CrosstabsCochran–Mantel–Haenszel test |
Description
The Cochran-Mantel-Haenszel test computes an odds ratio taking into account a confounding factor.
The test creates a series of two-by-two tables showing the association between a risk factor and outcome at different levels of a confounding factor, and computes a weighted average of the odds ratios across the strata (i.e. across subgroups or levels of the confounder).
How to enter data
For each case, the outcome, group and factor are entered on one row of the datasheet.
For example (adapted from https://sphweb.bumc.bu.edu/):
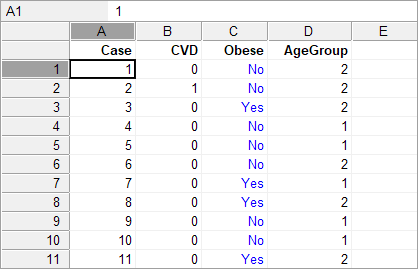
Outcome variable is CVD, group variable is Obese and factor variable is AgeGroup.
Required input
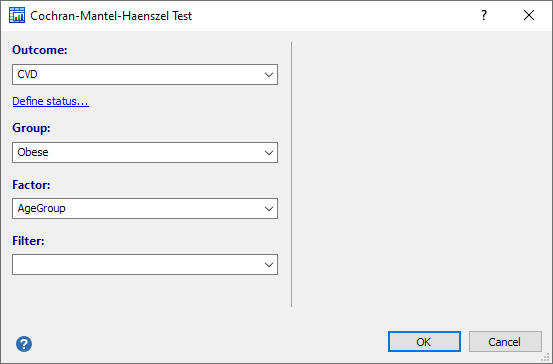
- Outcome: the Outcome variable must be binary or dichotomous, and should only contain data coded as 0 or 1. If your data are coded differently, you can use the Define status tool to recode your data.
- Group: select a variable with codes that identify 2 groups (e.g. treated and controls; obese and not obese, etc.)
- Factor: a categorical confounding factor (e.g. age groups).
- Filter: (optionally) enter a data filter in order to include only a selected subgroup of cases in the analysis.
Results
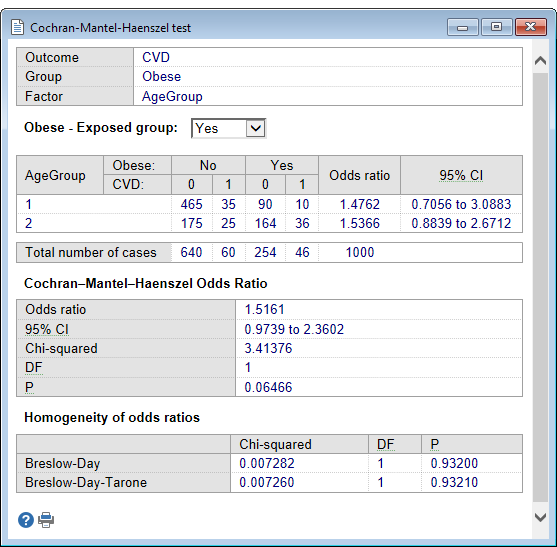
MedCalc reports the odds ratio with its 95% confidence interval in each stratum.
Next the program reports the weighted average of the odds ratio (the pooled odds ratio) across the different strata of the confounding factor, and its 95% confidence interval. MedCalc also reports the z-statistic and associated P-value. If P is less than 0.05 it can be concluded that the odds ratio is significantly different from 1 and that the odds in one group are significantly higher than in the other.
Tests of homogeneity of the odds ratios
MedCalc also performs the Breslow-Day and Breslow-Day-Tarone tests for homogeneity of the odds ratios across the different strata.
The null hypothesis for these tests is that the odds ratios are equal across the different strata. If P is less than 0.05 then the assumption of homogeneous odds ratios must be rejected.
For the tests of homogeneity to be valid, the sample size in each stratum should be rather large.
See also
External links
- Cochran–Mantel–Haenszel test on Wikipedia.