McNemar test on paired proportions

Command

Tests McNemar test

Description

The McNemar test is a test on a 2x2 classification table when the two classification factors are dependent, or when you want to test the difference between paired proportions, e.g. in studies in which patients serve as their own control, or in studies with "before and after" design.

In the example used by Bland (2000) 1319 schoolchildren were questioned on the prevalence of symptoms of severe cold at the age of 12 and again at the age of 14 years. At age 12, 356 (27%) children were reported to have severe colds in the past 12 months compared to 468 (35.5%) at age 14.

Was there a significant increase of the prevalence of severe cold?

Results

The data are entered as follows in the dialog box:

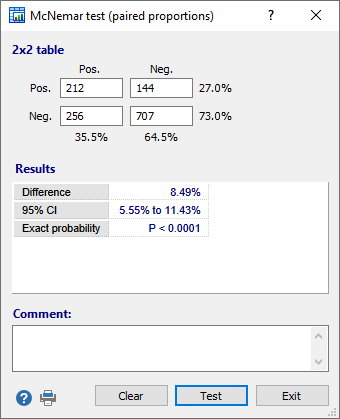
The program gives the difference between the proportions (expressed as a percentage) with 95% confidence interval. When the (two-sided) P-value is less than the conventional 0.05, the conclusion is that there is a significant difference between the two proportions.

In the example, the difference between the prevalence at age 12 and age 14 is 8.49% with 95% CI from 5.5% to 11.4%, and is highly significant (P<0.0001).

In the Comment input field you can enter a comment or conclusion that will be included on the printed report.

Note

If the number of discordant pairs (144 + 256 in the example) is less than or equal to 25, then the two-sided P-value is based on the cumulative binomial distribution. If the number of discordant pairs is more than 25 then a Chi-squared approximation with Yates' correction for continuity is used.

The 95% confidence interval is calculated according to Bland, 2000.

For the same test on raw (spreadsheet) data see McNemar test in the Statistics menu.

Literature

• Altman DG (1991) Practical statistics for medical research. London: Chapman and Hall.
• Bland M (2000) An introduction to medical statistics, 3rd ed. Oxford: Oxford University Press.

External links

• McNemar's test on Wikipedia.