MedCalc
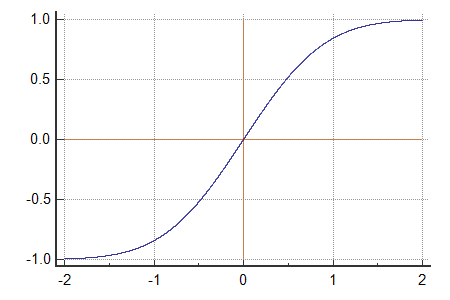
ERF function
Description
ERF(x) returns the error function integrated between zero and x.
$$\operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}\int_{0}^x e^{-t^2}\,\mathrm dt$$
$$\operatorname{erf}(x) = \frac{2}{\sqrt{\pi}}\int_{0}^x e^{-t^2}\,\mathrm dt$$ The argument x can be a real number or a matrix. When it is a matrix, the function returns a matrix with the same dimensions and with the ERF function applied to all elements.
Calculator
Graph
MedCalc Software Ltd
Digimizer