Cochran's Q test

Command:

Statistics Crosstabs Cochran's Q test

Description

Cochran's Q test is an extension to the McNemar test for related samples that provides a method for testing for differences between three or more matched sets of frequencies or proportions.

Example: 12 subjects are asked to perform 3 tasks. The outcome of each task is a dichotomous value, success or failure.

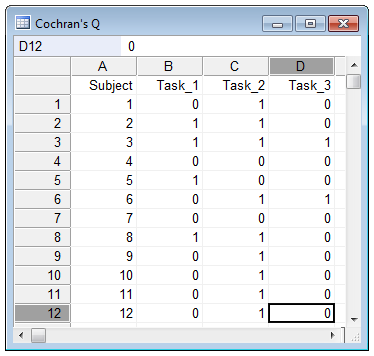
How to enter the data in the spreadsheet

The results are coded 0 for failure and 1 for success. In the example, subject 1 was successful in task 2 but failed tasks 1 and 3.

Required input

• Variables: the variables that contain the related observations. Data must be coded 0 to represent failure (or absence) and 1 to represent success (or presence).
• Filter: an optional filter to include only a selected subgroup of cases.
• Options
  • Significance level: the desired significance level for the post-hoc test. If the Cochran's Q test results in a P-value less than this significance level, MedCalc performs a test for pairwise comparison of variables according to Sheskin, 2004.

Results

Frequencies

This table gives the frequencies of the values coded 0 (meaning absence or failure) and 1 (meaning presence or success) in the different variables, the proportion (expressed as a percentage) of values coded 1

Since Cochran's Q test is for related samples, cases with missing observations for one or more of the variables are excluded from the analysis, and the number of cases is the same for each variable.

Cochran's Q test

The null hypothesis for the Cochran's Q test is that there are no differences between the variables (Sheskin, 2011). If the calculated probability is low (P less than the selected significance level) the null-hypothesis is rejected and it can be concluded that the proportions in at least 2 of the variables are significantly different from each other.

Multiple comparisons

When the Cochran's Q test is positive (P less than the selected significance level) then a minimum required difference for a significant difference between two proportions is calculated (Sheskin, 2011) and a table is displayed showing which of the proportions are significantly different from which other proportions.

Literature

• Sheskin DJ (2011) Handbook of parametric and non-parametric statistical procedures. 5^rd ed. Boca Raton: Chapman & Hall /CRC.

See also

• McNemar test

External links

• Cochran test on Wikipedia.